There are 2 tricks to balancing equations. First, spelling the technical word:
STOICHIOMETRY
Second, insuring that there are an equal number of atoms of each element on both sides of the equation, following the Law of Conservation of Mass.
The left side of a balanced equation is called the reactant(s). The right side is called the product(s).
The number of atoms is determined by multiplying the coefficients and subscripts.
To balance a chemical equation, change only the coefficients. This changes the number of elements or molecules used or produced without changing the element or molecular configuration itself.
Let’s balance an easy one...
We have 2 H’s on the left, so we need 2 on the right.And now the 2 Cl’s on the right match the 2 on the left. We’re in balance.
Here’s one with more steps:
on the right. We need 3 Pb’s on the left.
That gives us 12 Cl’s on the left, so we need the same number on the right.
TIP: Because the PO4 on the right is held together with parentheses, keep the PO4 on the left as a single entity as well.
TIP: In the balancing act, it is easier to make the final adjustments if there is a reactant that stands alone, a single element. Try to save these until last.
BALANCING with FRACTIONS
Even though this equation is technically "in balance," most teachers will want you to use only whole numbers as coefficients in chemical equations. Think about what you would do in a simple Algebra equation to get rid of a fraction. You'd multiply by a common denominator, so do the same here. Multiply ALL terms on BOTH SIDES by the denominator 2 to yield
TIP: The diatomic oxygen is so frequently involved in these fraction situations, that I try to "balance" the oxygens last.
Although these examples seem simple, the concept itself is simple also, regardless of how complicated a balancing question may appear. Just remember
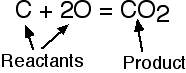






No comments:
Post a Comment