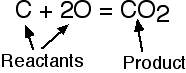VECTORS - What is a UNIT VECTOR?

By vector definition, a UNIT VECTOR is one in which the Magnitude equals 1.  (To review how to calculate Magnitude, refer to thenormalgenius.blogspot.com article "Vectors: What is Magnitude?," published on 8/19/13.) 

In working with vectors, it is sometimes simpler to use, or the equation calls for, a unit vector in standard position, i.e., originating from (0, 0).  Transforming a given vector into a friendly unit vector is easily envisioned by relating it to common algebra and geometry.

Think of a vector as the hypotenuse of a right triangle.  Draw sides parallel to the x axis and y axis.

If you start with a right triangle (5,12,13 for example) you would need to multiply the hypotenuse by its reciprocal (the multiplicative inverse - one of the properties of real numbers) in order to get it back to 1 (the multiplicative identity).  Dividing each of the legs by 13 (the hypotenuse) would give you the coordinates that would create a special right triangle with hypotenuse of 1 (5/13, 12/13, 1).

Try it with any right triangle:

         3,4,5 transformed to a right triangle with hypotenuse of
         length 1 would be   3/5, 4/5, 1.

         x, x√3, 2x gives you sides of length (x / 2x) or 1/2
         and (x√3 / 2x) or √3 / 2.

         These numbers sound a little familiar, don’t they?  I’m thinking Trigonometry -- Sine and Cosine of 30° and 60° angles.  And they coincide with the 30°- 60° - 90° right triangle that has sides equal to our example and the hypotenuse terminating on the circumference of a UNIT circle.


So when the study of vectors comes up and you are asked to determine whether a vector is a UNIT VECTOR, if the magnitude is 1, you know it is.  For scalar or vector components, you will want to change a vector INTO a UNIT VECTOR: divide x and y by the magnitude.  In the not-so-distant future, as part of the study of vectors in Precalculus, you'll discover equations which contain terms that look like this...

and you'll recognize the unit vectors.  A discussion of components will highlight these terms in an upcoming blog article. 

INDEX - THE NORMAL GENIUS ARTICLES

    CATEGORY   
DATE        TOPIC
----------------------------------------------------------------

    A BLOG INTRODUCTION

  3/19/10     THE NORMAL GENIUS

    ACT

  11/17/10   THE ACT SUGGESTS DEPRESSINGLY LOW BENCHMARKS FOR  COLLEGE READINESS
  7/3/10       4 MISCONCEPTIONS THAT MAY BE LIMITING YOUR ACT SCORE
  3/20/10     ACT LINK
  4/2/10       FOOD FOR THOUGHT (EATING YOUR WAY TO AND THROUGH THE ACT)
  3/29/10    QUICK TIPS FOR THE ACT
  7/27/10    SCHOLARSHIP AWARDS BASED ON YOUR ACT SCORE
  3/31/10    TIPS FOR ACT TEST DAY

    ACT - ENGLISH

  7/22/10    ACT: ENGLISH GRAMMAR
  3/19/10    IMPROVING ACT ENGLISH

    ACT - MATH

  3/24/10    ACT MATH CHECKLIST
  3/20/10    IMPROVING ACT MATH, PART ONE
  3/24/10    IMPROVING ACT MATH, PART 2
  3/22/10    REMEMBERING MATH FORMULAS

    ACT - READING

  3/25/10    IMPROVING ACT READING

    ACT - SCIENCE REASONING

  3/30/10    QUICK REVIEW OF ACT SCIENCE REASONING

    ACT - STUDY PLAN

  4/6/10      ACT - APRIL 10, 2010 (3 DAY STUDY PLAN)
  5/7/10      SELECTING A STUDY PLAN FOR THE ACT
  5/4/10      SOPHOMORES: GETTING READY TO STUDY FOR THE ACT
  3/26/10    START SLOWLY. WORK SMART. DO IT TODAY!
  5/31/11    STUDY FOR FINALS OR THE ACT?

    ALGEBRA

  7/21/13    QUICK STEPS TO COMPLETE THE SQUARE
  7/21/13    QUADRATIC EQUATIONS & THE PARABOLA (ALGEBRA II)
  7/18/10    PRE-SEMESTER REVIEW FOR ALGEBRA - PROPERTIES OF REAL NUMBERS
  2/8/11      LINEAR & ANGULAR VELOCITY
  7/21/13    ALGEBRA II: QUADRATIC EQUATIONS & THE PARABOLA
  7/21/13    QUICK STEPS TO COMPLETE THE SQUARE
  8/6/13      THE SUM OF TWO SQUARES - BREAK THE RULES
  8/6/13      IMAGINARY NUMBERS; TOOLS AND TRICKS  

    AP CALCULUS

  1/7/11      ORGANIZE YOUR RESOURCES (CALCULUS)
  3/31/11    SPECIAL STUDY FOR THE AP CALCULUS AB TEST
  4/27/11    AP CALCULUS AB
  5/1/11      WHAT THE TEACHERS ARE ASKING ABOUT AP CALC AB
  9/11/11    PREPARING FOR CALCULUS

    AP STATISTICS

  8/27/12    GETTING READY FOR AP STATISTICS - LEVELS OF MEASUREMENT
  8/18/12    GETTING READY FOR AP STATISTICS: VOCABULARY BASICS
  8/11/12    GETTING READY FOR AP STATISTICS: MEAN-MEDIAN-MODE
  8/4/12      GETTING READY FOR AP STATISTICS: COMMON GRAPHS

    CHEMISTRY

7/26/13    FIRST STEP IN CHEMISTRY - THE ATOM
8/19/13    BALANCING EQUATIONS

    COLLEGE

8/28/10    EARLY DECISION COLLEGE APPLICATION
10/4/10    PAYING FOR COLLEGE
6/2/11      A SPECTACULAR GPA IS NOT ENOUGH
1/22/12    PLANNING YOUR COLLEGE VISITS
1/9/12      PAYING FOR COLLEGE: SAVING MONEY ON TEXTBOOKS
4/1/10      EARN COLLEGE CREDIT WITH CLEP TESTS
7/25/10    ESSENTIAL STUDY MATERIALS FOR COLLEGE

    ELEMENTARY

1/17/12    TIPS FOR ELEMENTARY SCHOOL PARENTS: SHOULD WE HIRE A TUTOR?
8/9/10      NUMERACY: A FIRST STEP TOWARD PRESCHOOL MATHEMATICIANS
8/2/13      SINGAPORE MATH: USING BAR MODELS
8/9/13      SINGAPORE MATH: PARENTAL INVOLVEMENT
8/11/13    SINGAPORE MATH: AT-HOME RESOURCES

     EXAMS

5/4/10      FINAL EXAMS -- 3 WAYS TO PROCRASTINATE
5/27/10    FINALS - ACT - SUMMER!

    GENERAL MATH

8/8/10    GENERAL MATH    GET READY FOR THE NEXT LEVEL OF MATH

    GEOMETRY

1/4/11      THE AMBIGUOUS CASE (GEOMETRY & TRIG)
7/17/10    PREPARING FOR THE NEXT LEVEL OF MATH: GEOMETRY

    PRECALCULUS

3/30/11    COMPLEX NUMBERS..TO POLAR COORDINATES..TO RECTANGULAR COORDINATES
8/26/12    PARAMETRIC EQUATIONS: MATH ART
6/27/13    PARTIAL FRACTIONS - THE BASICS
6/26/13    VECTORS IN A NUTSHELL
6/27/13    PARTIAL FRACTIONS: the basics
8/19/13    VECTORS: WHAT IS MAGNITUDE
8/20/13    VECTORS: WHAT IS A UNIT VECTOR:

    PSAE

4/25/10    DO YOUR BEST ON THE PSAE
4/13/10    JUNIORS: 2 WEEKS TO THE PSAE STUDY PLAN
3/19/10    PRAIRIE STATE ACHIEVEMENT EXAM
3/31/10    SAMPLE QUESTIONS FOR THE PSAE (PRAIRIE STATE)
4/7/10      SENIORS! PSAE & GRADUATION

    PSAT

8/9/12    GETTING READY FOR THE PSAT

    SAT

2/17/11    TAKING THE SAT?

    STUDY SKILLS

8/22/10     FIRST DAY OF CLASS: COLLECT CONTACT INFORMATION
9/6/10       THE DIFFERENCE BETWEEN LEARNING & STUDYING
9/17/10     USING TESTS & QUIZZES TO MAXIMIZE YOUR STUDY PLAN
12/31/10    WHAT MOTIVATES THIS STUDENT?
1/14/11      TEST STRESS: CHICAOG TRIBUNE ARTICLE
2/18/11      MATH 911
9/13/11      PREPARE TO STUDY FOR SEMESTER FINALS
6/7/12       PAINLESS SUMMER GEEK
7/2/12       DOG DAYS MATH
5/19/10     STAYING MOTIVATED TO STUDY
7/8/10       SUMMER DATE BOOK = PSEUDO ASSIGNMENT PLANNER

    TEST TAKING

5/4/10      FINAL EXAMS -- 3 WAYS TO PROCRASTINATE
5/27/10    FINALS - ACT - SUMMER!  

    TRIGONOMETRY

6/28/13    TRIG SUM & DIFFERENCE IDENTITIES

VECTORS: WHAT IS MAGNITUDE?

VECTORS:  WHAT IS MAGNITUDE?

In terms of vectors, magnitude is the length of a line joining the origin to an ordered pair on the coordinate plane.  Its symbol is a number with a double line in front and in back....  ||V||

This is nothing new but you may not recognize the vector definition as the hypotenuse of a right triangle, calculated with the Pythagorean Theorem.

Let’s look at Vector G, (5, 12).  Find the point on a graph and draw a line from (0,0) to the point.

  Draw lines from the
  point to the x axis and      
  from there to the origin
  creating a right triangle.
                 
  Label these lines.

  Using the Pythagorean Theorem, the Hypotenuse is 13.

Since the equation for MAGNITUDE is

, magnitude is nothing more than the hypotenuse of a right triangle.  The magnitude of 

V (5, 12) = ||13||.

When you need to use Magnitude in a vector situation like finding the Norm, direction, unit vector, or scalar components, think PYTHAGOREAN THEOREM and HYPOTENUSE.

CHEMISTRY: BALANCING EQUATIONS

There are 2 tricks to balancing equations.  First, spelling the technical word:
                       STOICHIOMETRY

Second, insuring that there are an equal number of atoms of each element on both sides of the equation, following the Law of Conservation of Mass.

The left side of a balanced equation is called the reactant(s).  The right side is called the product(s).

The number of atoms is determined by multiplying the coefficients and subscripts.

To balance a chemical equation, change only the coefficients.  This changes the number of elements or molecules used or produced without changing the element or molecular configuration itself.

Let’s balance an easy one...

We have 2 H’s on the left, so we need 2 on the right.

And now the 2 Cl’s on the right match the 2 on the left.  We’re in balance.

Here’s one with more steps:

Start with the most complicated configuration, maybe Pb3
on the right.   We need 3 Pb’s on the left.

 

That gives us 12 Cl’s on the left, so we need the same number on the right.

Now there are 12 Na’s on the right, so we need the same number of Na atoms on the left. 

TIP:  Because the PO4 on the right is held together with parentheses, keep the PO4 on the left as a single entity as well.

And counting up the PO4’s shows that we have 16 on both the left and the right.  We’re in balance.  Notice that we didn’t have to write the coefficient ‘1’ because it is implied.

TIP:  In the balancing act, it is easier to make the final adjustments if there is a reactant that stands alone, a single element.  Try to save these until last.

BALANCING with FRACTIONS

Sometimes when balancing an equation, you'll wind up with terms that can't be split up.  What if you have O2 on one side and O3 on the other?

Assume that O3 is the more complicated entry so we need to get 3 oxygens from the diatomic O2 on the left.  Think of fractions.  We need one and a half O2s or 3/2.

Even though this equation is technically "in balance," most teachers will want you to use only whole numbers as coefficients in chemical equations.  Think about what you would do in a simple Algebra equation to get rid of a fraction.  You'd multiply by a common denominator, so do the same here.  Multiply ALL terms on BOTH SIDES by the denominator 2 to yield

TIP:  The diatomic oxygen is so frequently involved in these fraction situations, that I try to "balance" the oxygens last.  

Although these examples seem simple, the concept itself is simple also, regardless of how complicated a balancing question may appear.  Just remember

MATTER CAN BE NEITHER CREATED NOR DESTROYED.

SINGAPORE MATH: AT-HOME RESOURCES

WARNING:  THERE IS MORE TO SINGAPORE MATH THAN THE CLASSROOM

Even critics of the Singapore Math program could not object to the proclaimed objectives of teaching students to the mastery level, using real world situations for problem solving, and encouraging communication in math.  After all, these same goals have been recommended by the National Council of Teachers of Math for decades.  Everyone interested in math wants our children to love math, not just tolerate it through 11 or 12 years of compulsory education.

And even the critics may not call enough attention to the need for out-of-school support if students are to achieve that mastery of basic arithmetic concepts.  The Singapore Math classroom curriculum stresses conceptual understanding to the delight of advocates, but procedural and skills proficiencies are often the under-reported secondary requirements that critics demand and that are an integral part of Singapore's education program. 

Unlike the American system in which “school” ends at 2:30 and is replaced by dance class, sports, and other extracurricular activities, in the country which inspired Singapore Math, nearly every student receives supplementary homework assignments, as well as additional rehearsal through math clubs and “after school tuition classes” like our tutoring services.  The reported 1995 (http://nces.ed.gov/pubs99/1999081.pdf) through 2007 (http://nces.ed.gov/timss/table07_1.asp) math success in Singapore may be more heavily dependent on the cultural significance placed on education than we realize.

With this possibility as our hypothesis, effective implementation of Singapore Math in American schools will require at least moderate changes to our priorities.  It will be necessary that after school activities devote more time and effort to the repetitive work -- those dreaded “math facts” like multiplication tables.

Practice in basic computation can be tedious for both parent and student.  Multiple worksheets with 25, 50, 100 problems are boring, to be generous.  A parent verbally making up sample problems is demanding.  The chances are that none of us is going to follow through long enough for our kids to gain the level of skill that we would like.  We need a helper.

Tutoring Resources uses a game we call “War on Integers” which is played like the familiar card game War.  Contact us at www.tutoring-resources.com for a free copy of instructions for playing with addition, subtraction, multiplication, or division.  The game encourages the student to practice in a fun way that doesn’t depend on age or grade level to “win” and promotes the much needed rehearsal.

The internet is another readily available resource.  There are many sites that provide colorful, entertaining games for students from kindergarten through sixth grade and even higher.  My personal favorite (because I played it with my own kids back in the day) is NUMBER MUNCHERS.  I have it on floppy disk (I did mention that it was “back in the day”) but for today’s electronically-literate youth, it’s available for iTunes, iPhone, and iPad Touch.

Other sites to explore include
www.wallofgame.com  (Number Munchers is available on this site.)

www.Sheppardssoftware.com  (A listing of several useful sites.)

www.IXL.com  (This one makes it easy to access appropriate games by grade level and even goes through Algebra.)

www.Cool.math-games.com (This site may not be as distracting for kids who are accustomed to websites as it was for me, but I would not recommend it for anyone with focus and concentration issues.)

As a general rule, games will require dexterity with either arrows or a mouse.  I found them all easier to play on a desktop than laptop computer.

Want more suggestions?  Just search the web for ‘math games’ and be prepared to spend considerable time checking out a myriad of sites that might appeal to the specific interests of your student -- and playing a few yourself.  I lost more than a few minutes on the pop-up www.ahhhhh.com, which is apparently a soft drink website ad, as mezmerizing as it is subliminal.

If our kids are going to get the promised rewards from Singapore Math, parents need to make it a point to provide the supplements that will fill in the gaps.  Luckily, plenty of resources are available to make our job easier. 

SINGAPORE MATH: PARENTAL INVOLVEMENT

So your school district is all in a lather over Singapore Math.  Some are dead set against the changes coming in the Fall and others are so enamored that they seem almost manic.  This is a common scenario:  two sides, both at the extremes.  Critics and advocates alike will implement the new methods, procedures, and texts like scientists conducting an experiment.  The classroom is the lab.  Results will be evaluated somewhere down the line and assessments made about the effectiveness of the program.  It has happened before with “new math,” Everyday Math, and many other attempts at improvement that have resulted in both success and failure. 

But YOU are the parent and what happens to, for, and with your child is a permanent fixture of his or her education with important future ramifications. To YOU this “experiment” MUST WORK.  Supporters of Singapore Math do not hesitate to stress the importance of parental support for successful implementation.  Some suggest that after-school tutorials and homework are integral factors in the reported success of elementary students in Singapore.  If you are among the group of the hesitant, unsure of your own math knowledge and ability to adjust to Singapore Math, this article will help you become a competent homework assistant.



--------------------------------------------------------------

TIPS FOR PARENTS NEW TO SINGAPORE MATH

1.  Many of the “informational” publications about SM are lean on specifics.  You’ll hear that the Singapore Math program as amended for American Schools teaches mathematical concepts from concrete through pictorial to abstract, devoting more time to fewer topics and stressing “mastery.”  This limited information seems to me to be more of a sales pitch than useful data. 

It is up to the parent to drill down to details that will help each student to learn the math fundamentals.

For example, here is the sequence of study for the first week or two of each grade:
    Kindergarten:      Numbers to 5
    First Grade:         Numbers to 10
    Second:              Numbers to 1,000
    Third:                  Numbers to 10,000
    Fourth:                Place Value of Whole Numbers
    Fifth:                   Whole Numbers
    Sixth:                  Positive Numbers/Number Line

With this information in mind, you can help prepare your student for the first few days of school by reviewing the numbers that will be covered.

2.  To ensure that you are in the loop throughout the school year, be sure you are receiving the “School-to-Home Connections” newsletters from the teacher at the beginning of each chapter.  These include a summary of the upcoming lessons, vocabulary, and an activity to support learning at home.  The newsletters are available to the teacher as prewritten resources which can be printed for general distribution, emailed, or posted on the school’s homework website. (Sixth through eighth grade newsletters are called “Family Letters.”)

3.  Many of the “new techniques” used in SM are similar to systems used in the 1950s and 1960s.  That’s a little before the grammar school dates of most of today’s parents, but here is a tremendous opportunity to get gramma and grampa involved.  Ask them about “friendly numbers.”

I am of that era and remember breaking large numbers into workable groups. (In fact, I still use this system for mental math, which is a chore for me rather than a talent.) For example, studies have shown that most people can “picture” numbers up to 6 in patterns found on playing cards.  The number 7 becomes more difficult to envision, but it can be broken up into 5 and 2.  Adding 5 and 7 is the same as adding 5 plus 5 plus 2.  Adding 5s is a familiar pattern; 5 + 5 = 10.  Add another 2 to find the sum of 5  + 7.  In Singapore Math, this is called “adding with regrouping.” Learning the process is facilitated by using manipulatives.

Subtracting with regrouping is similar.   Seven can also be broken up into 3 and 4.  So 13 - 7 becomes 13 - 3 to get 10 and then subtracting 10 - 4.  Ten is the friendly number in this case.

For early elementary students, using manipulatives to find number patterns (called number families in some very old textbooks) is a common practice.**

**  Manipulative “dots” are available free of charge to fans of this blog.  Become a fan and send a request for a set of 100 Dots through the comments section that follows this article or email tutoring.resources@yahoo.com

4.  Singapore Math uses “place value mats” as early as first grade.  The classroom teacher should have a template which can be copied and distributed to families, or you can easily make your own by replicating the following pattern.  Columns should be long enough to accommodate 5 manipulative dots (breaking 10 up into friendly 5s).  Laminating the mat will ensure that it holds up to 6 years of single student use or as a sibling hand-me-down.  At the second grade level you’ll want headings for thousands, third grade ten thousands.

5.  ADDITION (OR SUBTRACTION) WITH RENAMING are the SM terms for “carry the one”  and “borrow” with which you might be more familiar.  Be sure to review the vocabulary from the School-to-Home newsletter and ask the teacher if the connection to the math you know is not immediately obvious.

6.  After manipulatives, SM might move to drawings to transfer tactile knowledge to the more conceptual/visual format.  You may want to practice setting up word problems using this system.  It is not complicated when you've mastered the routine steps for creating bar models.  Check out The Normal Genius blog, "Singapore Math: Using Bar Models," posted on August 2, 2013.

7.  Other techniques that SM uses to engage students and stimulate higher level thinking include a heavy use of word problems (called “practical applications” in some older textbooks and college courses) and classroom discussions.  The format frequently presents a story that would use some form of math to solve a problem, let the students work independently or in groups to “think it out,” followed by presentations of their solutions.  This practice has long been supported by the National Council of Teachers of Math which emphasizes both real life situation applications and the importance of communication in mathematics either through speaking or writing.  It encourages students to identify and recognize their own problem solving thinking, a metacognitive element of learning.

You can help your student prepare for this task by practicing explaining the steps to a solution for sample homework problems.  Your own ability to model the process could be a valuable asset for your student.

8.  Thinking through problems is only part of the SM formula.  Rehearsal of basic math facts is still required but will need to take place at home.  Ask the teacher for supplemental materials outside of the workbook exercises.  Try chanting the multiplication tables (like you did to learn them) while throwing a ball back and forth or bouncing it on the floor for students who need to move while learning.  Or chant to a particular beat for the musically inclined.  Use your imagination to design drills that meet the specific needs of your unique student.

9.  Not necessarily part of the Singapore Math program, but a useful tool for upper elementary students when word problems can become quite complicated, is a strategy I call “Is that your final answer?”  It sets the framework for what the answer will look like, set up at the beginning of the problem solving process and insuring that the student doesn’t stop too soon or go down a blind alley while working out a solution.  In either math symbols (4X = ___ ) or words (4 pencils cost ___ ), the practice is similar to checking the question after working through the math.

---------------------------------------------------
So your school district is all in a lather over Singapore Math.  But you are calm, cool, and collected because you are prepared to help your student make the most of the program and maybe even gain confidence in your own math skills at the same time.

The SUM of Two Squares -- BREAK THE RULES!

Here’s something nobody else in your Algebra II class (maybe even the teacher) will know.  (Do not try to be the wise-cracker until you're ready to PROVE that this works!!)

Since first learning to factor, we've been told that "the rules” are... you

    -  CAN factor the DIFFERENCE OF TWO SQUARES (referred to by some texts as ‘DOTS’)  into conjugates.....

    x^2 - 16 = (x - 4)(x + 4)

    - CAN NOT factor the SUM OF TWO SQUARES.  This second admonition is true when the instructions say "factor completely across the integers" because, as you are about to see, the answers are NOT integers.

BUT You CAN factor the sum of two squares if you've studied imaginary numbers and know a simple little TRICK.

        You will still use conjugates, but there needs to be an i in the second term of each binomial.....

    x^2 + 16 = (x - 4i)(x + 4i)

Why does it work?  Because when these two binomials are FOILed, the middle terms (O and I) cancel each other out.  AND since i^2 is simply -1, the multiplication of the last terms gives you the task of subtracting a negative number, which is simplified to ADDING!!

Try factoring these sums of perfect squares and FOIL the binomials to verify that you actually CAN “break the old rules” when you know enough math!!

PROBLEM A:     p2 + 64

PROBLEM B:     121 + y2 (hint: use the commutative property first and attach the i to the square root of 121)

PROBLEM C:     x2 + 36 y2

---------------------------------------------------
 And this concludes the demonstration of how a math nerd can break all the "rules" and get away with it, mathematically speaking!!

IMAGINARY NUMBERS, TOOLS AND TRICKS

I tell my students that mathematicians don't like situations in which they can't find an answer, so when the quadratic equation so frequently comes up with a negative discriminant, it drives them crazy.  ("You can't take the square root of a negative number!!," emphatically warns the arithmetic teacher.)

As a mathematical cure for the insanity, someone introduced the "imaginary" number.  It's like your little brother's imaginary friend; you can see it plainly in your head, use it for all kinds of activities and excuses, but nobody else can actually put their finger on it.  It's purpose is to take the negativity out of a square root and make the problem solvable.

√ (-49) = √(-1)√(49)
So make the square root of negative one equal 'i' and the problem disappears.

√ (-49) = 7i

And with just that little piece of information, I'm ready for the quiz.
----------------------------------------------------------

That was all very easy, so let's look at some "tricks."

If   i = √(-1)
then i^2 = -1
and i^3 = -1 √(-1) = -1i = -i
and i^4 = (-1)(-1) = 1

So any i raised to a power evenly divisible by 4 equals 1.  This reminds me of the trick about 0 as an exponent:  (almost) Any base raised to the zero power equals 1.  I love seeing that on tests in problems that look like...

     (43x^90 + 103x^80y^15 - 74y^101) ^ 0

                    = 1

With i's, breaking it into parts equal to i^4 is like taking out '1' many, many times, and 1 times 1 times 1....still equals one.

To find i to any other power, just attach the remainder to i.
     i^81 = i^1         81÷ 4 = 20 (who cares?) with a remainder of 1
     i^ 27 = i^3        27 ÷ 4 = 6 (useless information) with a remainder of 3
     i^98 = i^2= -1   98 ÷ 4 = 24 (yawn) with a remainder of 2
-----------------------------------------------------------

How easy was THAT?!?  Give it to me on a quiz and I'm sure to get that point!!

Multiplying conjugates that contain imaginary numbers is also a no brainer.  The middle terms cancel each other out and you're left with squaring i to make it a rational number.

     (x - 4i)(x + 4i) = x^2 – 4ix + 4ix - 16i^2
          Let i^2 = –1
     (x – 4i)(x+ 4i) = x^2 + 16  (Catch the next blog on "breaking rules.")

This little trick comes in handy when you are confronted with a complex number in the denominator:

And BEHOLD...the denominator turns into an integer.

---------------------------------------------------------

There's one more trick that is handy for the tool kit of aspiring Math nerds and others who want to be a pain in the side of any math teacher.  But that one will be posted separately so you have to look for it and prove that you're really committed to creating waves, because it is BREAKING THE RULES!!! (sort of)

SINGAPORE MATH: USING BAR MODELS

PARENTS’ GUIDE TO HELPING STUDENTS DRAW BAR MODELS

My mother still laments the transition to “the New Math” in the elementary curriculum between my sister’s experience and my own -- and THAT was 50 years ago!!  It is understandable that parents (and some teachers) are hesitant when something new and radical is implemented in an otherwise comfortably familiar class.

This is the state of affairs in more and more school districts as the educational system searches for ways to improve America’s lack of stellar performance in science, technology, engineering, and math (STEM) programs.  Statistics over the past decade report that very young children in Singapore ranked first in the world in mathematics (Trends in International Mathematics and Science Study (TIMSS)-2003), initiating a wave of interest in the current edition of the newest math experiment, Singapore Math.

I have one suggestion for parents who are feeling unsure of their ability to help their students make the transition to Singapore Math.

                DO NOT PANIC!! 

Although jumping head first into a new method of “thinking math” can seem an impossible challenge, the “Bar Modeling” method used to visualize word problems in Singapore Math is less complicated than it “appears.”  And “appears” is exactly the right term to use because the Bar Method is intended to be a visual collection of details from a word problem.  It is probably most applicable for students who are visually oriented, Visual Learners, but many schools will and are presenting the method to all students, regardless of their learning style.  In the elementary grades, the philosophy is that the very young are not capable of thinking abstractly and require concrete exemplars.  Supporters of Singapore Math profess that the system is a superior way to lead children to a strong foundation for understanding the basics of math.

For parents new to the subject, the “8 Step Approach” proffered by recognized experts on Singapore Math could be helpful if not somewhat cumbersome.  Boiling the process down to a more streamlined form will provide every parent with the basics to competently help with homework.
         1.  Draw a rectangle.
         2.  Divide it into boxes.
         3.  Color in some boxes.
         4.  Divide into smaller boxes.
         5.  Count.

While implementing Singapore Math, think of denominators.  They form the basis for dividing up the BARS.  The process can most easily be described through example.

Lily makes macramé bracelets to sell at the local flee market.  Last weekend, she sold 3/5 of her jewelry on Saturday and 1/4 of the rest of her inventory on Sunday.  If she sold 20 more bracelets on Saturday than she did on Sunday, how many bracelets did she have in the first place.

If 20 bracelets are in the 5 dotted BARS, there are 4 bracelets in each BAR.  We're still using fractional division here. There are now a total of 5 times 2, or 10 bars, each holding 4 bracelets, so there were 40 bracelets at the beginning of the weekend. The division of BARS is relatively simplistic in this example.

Here’s the “traditional” format for writing equations to solve this problem.  It relies on direct translations of the instructions in the word problem to “mathese,” a step that is frequently skipped by students in high school courses, but which can add points on an AP test.

     X = total bracelets
     Saturday Sales = 3/ 5 X
     Sunday Sales = 1/ 4(1 X - 3/ 5 X) = 1/4 (2/ 5 X) = 2/ 20 X
     Saturday Sales = Sunday Sales + 20

         3/ 5 X = 2/ 20 X + 20
         12/ 20 X = 2/ 20 X + 20
         12/ 20 X - 2/ 20 X = 20
         10/ 20 X = 20
         X = 20 (20/ 10) = 40 bracelets


But what about divisions that are more complicated.  A few minor changes in the numbers and dividing the remaining bars seems confusing, but there’s a simple technique.

Lily makes macramé bracelets to sell at the local flee market.  Last weekend, she sold 3/5 of her jewelry on Saturday and 1/3 of the rest of her inventory on Sunday.  If she sold 14 more bracelets on Saturday than she did on Sunday, how many bracelets did she have in the first place.

In the first problem, dividing the remaining BARS was a simple task of dividing each into 2.  This time, instead of dividing into simple fourths, we need to divide the two BARS into three and make similar divisions to Saturday’s sales.  How do you divide 2s into 3s? The least complicated way to create subdivisions is to divide EACH BAR into three pieces.  This process is not unlike finding a common denominator.  Notice that the 2 pieces become 6 smaller parts.

Since there are still 7 dotted BARS in Saturday's group prepresenting 14 bracelets, each new subdivision holds 2 bracelets.  There are now 15 subdivisions in all, so Lily had 30 bracelets to sell at the flee market. 

The traditional solution looks like this:

     X = total bracelets
     Saturday Sales = 3/ 5 X
     Sunday Sales = 1/ 3 (2/ 5 X) = 2/ 15 X
     Saturday Sales = Sunday Sales + 14
         3/ 5 X = 2/ 15 X + 14
         9/ 15 X = 2/ 15 X + 14

         9/ 15 X - 2/ 15 X = 14

         7/ 15 X = 14
         X = 14 (15/ 7) = 30 bracelets to sell in the first place

The problems demonstrated so far are quite complicated and would appear in Singapore Math around the fifth grade level.  If the student started the process earlier in elementary school, the BAR drawings would be a familiar format that may have started with a very, very simple example of adding fractions like this one...

Lily makes lemonade to sell at a booth in her driveway.  She uses all of her ingredients to make lemonade on Saturday and sells 3/5 of her supply on Saturday and 1/3 of the remainder on Sunday. What fraction of the original lemonade was left at the end of the weekend?

Steps:
1.  Divide whole into 5 parts (to
represent the denominator of 3/ 5)

2.  Count out 3 BARS for Saturday.
3.  Divide the remaining BARS into thirds (for 1/ 3 of remaining juice)
4.  Divide Saturday’s BARS similarly.
5.  Mark out 2/6 of Sunday’s subBARS
6.  Mark out the same amount on Saturday (only because it’s become a habit by now, even though it is NOT NECESSARY).
7.  Count the subBARS which have NOT been marked out.

 4/15 of the original lemonade was left over after sales on Sunday.

The traditional solution looks like....

     X = total lemonade
     Saturday Sales = 3/ 5 X
     Sunday Sales = 1/ 3 (2/ 5 X) = 2/ 15 X

     Saturday Sales + Sunday Sales = 3/ 5 X + 2/ 15 X = 11/ 15 X
     Total lemonade - Sales = 1X - 11/ 15 X = 4/ 15 X

IS SINGAPORE MATH WORTH THE HYPE? 

CON:  I’m really not sure whether this method makes fractions easier for students to learn and eventually manipulate.  My own first exposure to fractions was pre-New Math, so I’ve been experimenting with Singapore Math just like everyone else.  At first, CREATING more fractions seems counterintuitive and may cause consternation in the hearts of parents and students.

PRO:  It may be reassuring to parents to find the Singapore approach very similar to one we’ve used for years to teach early elementary numeracy by using cardboard fraction bars (notice the similarity in terminology) or Legos.  In fact, there are commercial Lego kits to use in teaching Singapore Math.  I am certainly delighted to see the attempt to make fractions into friendly things that can be expressed visually for those who think that way, especially since we use rational expressions to great extent in Algebra, Trigonometry, and Calculus.

CON:  Since experts contend that young students are unable to grasp the theoretic concepts, why aren’t they as concerned with those children’s manual dexterity in creating BARS?  The BAR modeling concept relies on  EQUAL divisions.  Consider this potential student drawing:

  Is the concept of 1/4 accurately visualized?  Will sloppy drawing confuse the issue of equivalent fractions?

PRO:  I’m in favor of any system which makes collecting and using details from word problems a major focus of study.  Personally, I like “just working problems,” but I haven’t found many students who share the feeling.  The current emphasis in STEM study is the usability of skills, requiring practical applications presented through word problems.  Singapore Math certainly places a premium on word problems and THAT can be a major plus.

CON:  I am not convinced, however, that the time required for accurate artistic renderings is worthwhile in the upper grades.  I’m positive I’d never use the system on a timed test like the ACT.  The statistics which suggest that Singapore’s educational system for teaching math is superior only measures performance at the fourth and eighth grade levels, and at some point, students will have to abandon the visual representations in favor of international conventions. I’m eager to observe how the transition from Singapore Math to traditional solutions will be made.

PRO:  BAR modeling could prove to be a useful key for helping VISUAL LEARNERS to develop an intrinsic understanding of fractions and to translate the details of some word problems.  Singapore Math offers opportunities for revisions that could inspire MANUAL LEARNERS by using clay, for example, and cutting 3-d rectangular prisms into subdivisions.  Innovative teachers might experiment with modifications that are so successful that the next new approach could be called “American Math.”  For the time being, I plan to get as much traction from the latest new system as I can. 

If you find interesting problems from your student's class, please share them in the comments.  

The greater the number of unique examples, 

the deeper the understanding.