VECTORS IN A NUTSHELL

       

WHY SHOULD I LEARN ABOUT VECTORS?

After so many years of working with the same curriculum, I sometimes need to be convinced of the benefit of learning something new.  I’m relatively sure many students feel the same way.  So when it came time to expand the curriculum to include vectors, I was resistant.  However, a little research pointed out that many of my interests could benefit from understanding vectors.

Of course, vectors are found in science and engineering, but those disciplines have never prompted me to learn vectors in the past.  A math class problem made me realize that the football quarterback is thinking in vectors when calculating where to throw the ball and how much force to use to get it to the intended receiver.  In my youth, I thought of being a weather forecaster, and now I discover that vectors are needed to draw wind maps.  Fats Domino, famous pool player, was expert in calculating vectors to “drop the 5 ball in the corner pocket” by first hitting it with the 10 ball.  In helping a student study for the police exam, I found that investigators use vectors to describe the details of an accident.

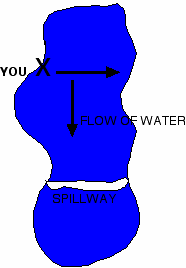
Our trigonometric experience with triangles is useful in determining the outcome of opposing forces described as vectors.  For example, you want to swim across the Rock River.  There's a spillway about 100 yards downstream from where you are.  Considering the rate at which the water is flowing, can you swim to the other side before falling over the spillway and possibly incurring bodily harm? We never thought about this when we, as teens, were swimming across the river, but maybe we should have.

Wow, maybe vectors ARE worth learning to prepare for a wide variety of experiences and careers.  So let’s get started...

WHAT IS A VECTOR?

In its most general description, a vector is a line which demonstrates 2 characteristics:
                LENGTH (called "magnitude")
                and
                DIRECTION, indicated by an arrow head at its terminal end

Here's a vector drawn on the coordinate plane:

It starts a S(1,2) and ends at T(6,5).

To find the Cartesian coordinates that would name this vector if it started at (0,0), we would subtract:
                   T - S
and, in this example,  get  (5,3).  From these coordinates, we can calculate the MAGNITUDE by using the Pythagorean Theorem:

                  magnitude, ||ST|| = √ (x^2 + y^2) = √ (5^2 + 3^2) = √( 34)

           Finding ||ST|| from the original components is just like the distance formula:
                                       ||ST|| = √[(6-1)^2 + (5-2)^2]

The coordinates also give us all the information necessary to determine the angle, or direction, of the vector:

                  Tan θ = y/x     or the longer way Tan θ = (5-2)/(6-1)
                                      Doesn’t that fraction look just like SLOPE?  

When the magnitude and direction are given as polar coordinates, (r, θ)....

....the x and y coordinates can be calculated using these equations:
              x = r(cos θ)
              y = r(sin θ)    (Remember from Trig....Cosine is the x axis, Sine is the y axis) 

COMPUTATIONS WITH VECTORS

ADDITION

Let Vector A = (3,8)
      Vector B = (2,4)

To add Vector A and Vector B for a RESULTANT Vector C:

    Add the x values.........3 + 2 = 5
    Add the y values.........8 + 4 = 12

The RESULTANT Vector C = (5,12)

with magnitude of 13.

SUBTRACTION

To subtract Vector B from Vector A for a RESULTANT Vector D:

  

     Subtract the x values.....3 - 2 = 1

     Subtract the y values.....8 - 4 = 4...........Vector D = (1,4) with magnitude of √17

SCALAR MULTIPLICATION

To increase a Vector by a given scale, multiply both x and y by the scale.

     5(Vector A) = 5(3,8) = (15,40)

DOT PRODUCT versus CROSS PRODUCT

DOT PRODUCT (sometimes called the SCALAR PRODUCT or INNER PRODUCT) is found by multiplying the x values together and the y values together and adding the two products.  The answer is a single number.

     Vector A (3,8) • Vector B (2,4) = (3)(2) + (8)(4) = 6 + 32 = 38

If the sum equals 0, the two lines are PERPENDICULAR.  WHY?!?
    Well, let's look at what we know from Algebra I.  If the slopes of two lines are opposite inverses, then the lines are perpendicular.  So, multiplying (as in the Dot Product) the numerator of two perpendicular slopes would be the additive inverse (opposite) of the product of the denominators.  Adding the two would result in a sum of zero.....ergo perpendicular lines. 

CROSS PRODUCT (sometimes called the OUTER PRODUCT)

     (Vector A) X (Vector B) = ||A||•||B||

Although Cross Product will not appear until later in the program, it is important to recognize the differences now, when we're talking about the Dot Product.  Dot Product can be completed on two vectors in a single plane; the Cross Product is only applicable in 3 dimensions.  It provides a vector perpendicular to two other vectors in a plane -- a vector perpendicular to that plane.  Cross Product involves matrices, so brush up on Cramer's Rule and determinants before we get to it later in the curriculum.

OTHER UPCOMING ISSUES WITH VECTORS 

Once we're comfortable with these basic vector concepts, we can explore more complex issues like unit vectors, resolving vectors into their components, vectors in 3 dimensions, and representing scalar values of unit vectors using i, j, and k.