PRE-SEMESTER REVIEW FOR ALGEBRA -- PROPERTIES OF REAL NUMBERS

(In the Algebra classroom, it is often not stressed that the steps taken in solving an equation are based on the properties of real numbers. Every Algebra student has heard the terms and sometimes the response to stimulus like the word “distribute” mirrors Pavlov’s dogs*. The point that is missed, in my opinion, is the use of properties as reasons for taking a solution step, which would be an introductory activity for 2-column proof in geometry and logic. Tutoring Resources has an activity that uses simple algebra equations to demonstrate 2-column proof. Visit the website www.tutoring-resources.com to request a copy.)

For students taking Algebra next semester, there is a good chance that properties will be tested within the first week or two of school. So, let’s review Properties and see how to think about them while working algebra problems.

COMMUTATIVE PROPERTY:
Think about the commuters on a train. They get on in various cities along the line, but they can get off in any order. The Commutative Property says that you can add or multiply in any order.

ASSOCIATIVE PROPERTY:
Think about standing in line at a concert. You come with several friends and you’re chatting amiably when you notice a classmate 50 people behind you in line. You may NOT give that person skips in line (like the commutative property). But if the kid behind you says hello, it’s okay to turn around and talk with that person also. You can’t let an interloper in line, but you CAN associate with the people around you. This is the Associative Property which also says you can add or multiply in any order.

DISTRIBUTIVE PROPERTY:
I like the expanded the title of this property: The distributive property of multiplication OVER addition and subtraction. It actually explains that the coefficient jumps OVER the parentheses and multiplies each of the addends or subtrahends before they are added or subtracted.

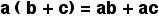IDENTITIES:
Identical twins are exactly the same. Identical terms are also exactly the same. There is a way to get exactly the same term in adding and multiplying.

ADDITIVE IDENTITY:

Think -- What would I add to a number to get exactly the same number back again?

MULTIPLICATIVE IDENTITY:

Think -- What would I multiply times a number to get the same number back again?

INVERSES:
Using the Identities, we can also know the inverses intuitively.

ADDITIVE INVERSE:

In arithmetic, you called this the “opposite.” Think -- what would I add to a number to get the Additive
Identify of 0?

MULTIPLICATIVE INVERSE:

You might have previously called this the “reciprocal.” Think -- what would I multiply a number by to get
the Multiplicative Identify of 1?
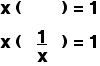SUBSTITUTION:
In brief, if 2 terms are equal, then either one can be used for the other.

EQUALITY:
These properties are the steps in equation solving that let you move things across the equal sign. Think -- whatever I do to one side of the equation, I have to do to the other.

ADDITIVE EQUALITY:

MULTIPLICATIVE EQUALITY:

Do you see a similarity between the equations shown in Substitution and those under Equality? Can you explain why?

--------------------------
Now, if you’re thinking that I just spent over an hour uploading this lesson for your benefit alone, you’d be mistaken. It’s not just students who should review previous knowledge before beginning the new semester. Teachers also look over previous work and review concepts, just to be sure we aren’t forgetting something. While a student may forget because of LACK of use, a teacher often forgets because of too much FAMILIARITY. It would be easy to overlook one of these properties, just because it’s always been there. It’s like forgetting to put a pencil in your backpack because there’s always been one there in the past, so you expect it to be there every time.

Just be happy that you’re not the teacher. While you are reviewing for only one class, your teacher is probably preparing for 2 or 3 or even 4 diverse courses!


*"Pavlov's Dogs" is a common reference to an experiment in the 1890’s by Ivan Pavlov in which he rang a bell immediately preceding offering food to the dogs in his study. The food made the dogs salivate. Eventually, just by ringing the bell, the dogs associated the sound with the upcoming food and began to salivate even when food was not offered. The reference to Pavlov suggests that a conditioned response can be elicited by repeated association of two unrelated things: in this case, multiplying a coefficient with each addend inside parentheses.